Contrainte dans l'acier de béton armé en fonction de sa déformation, σ_s

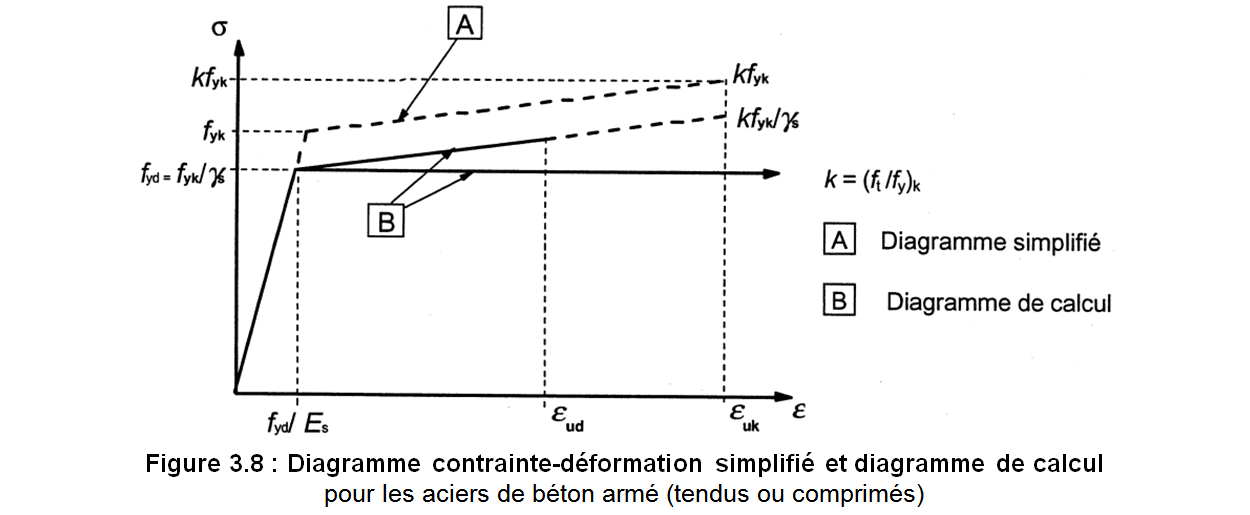
Pour un calcul courant, l'une ou l'autre des hypothèses suivantes peut être faite (voir Figure 3.8) :

a) branche supérieure inclinée, avec une limite de déformation égale à ε_ud et une contrainte maximale kf_yk/γ_S pour ε_uk, avec k = (f_t/f_y)_k,

b) branche supérieure horizontale, sans nécessité de vérifier la limite de déformation.

où :

f_yk

est la limite d'élasticité de l'acier de béton armé, voir § 3.2.2 (3)P

γ_S

est le cœfficient partiel relatif l'acier de béton armé, voir § 2.4.2.4 (1).

k

est la propriété de ductilité, voir le Tableau C.1

ε_uk

est la valeur caractéristique de la déformation relative de l'acier de béton armé sous charge maximale, voir le Tableau C.1

E_s

est le module d'élasticité de calcul de l'acier de béton, voir § 3.2.7 (4)

f_yd

Limite d'élasticité de calcul de l'acier de béton armé, f_yd = f_yk/γ_S

ε_ud

est la valeur de calcul de la déformation relative de l'acier de béton armé sous charge maximale, ε_ud  = Coef(ε_ud)⋅ε_uk, voir § 3.2.7 (2) pour la valeur de Coef(ε_ud).

Si ε_s ≤ ε_se (avec ε_se = f_yd/E_s), la contrainte dans l'acier de béton armé σ_s = E_s⋅ε_s.

Si ε_se < ε_s ≤ ε_ud, la contrainte dans l'acier de béton armé σ_s est égale à :

• f_yd + (ε_s - ε_se)⋅(kf_yk - f_yk)/(ε_uk - f_yk/E_s) pour la branche supérieure inclinée,
• f_yd pour la branche supérieure horizontale.