b1. Méthode de calcul des armatures longitudinales d'une section rectangulaire en flexion simple à l'ELU, Asc et As
Eurocode 2 - Calcul des sections de béton
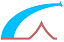
Hypothèses
1. La section plane reste plane après déformation. Ainsi, la distribution des déformations est linéaire à travers la section.
2. Les armatures subissent les mêmes déformations que le béton adjacent.
3. La résistance du béton à la traction est négligée.
4. Un diagramme rectangulaire de compression dans le béton est admis, voir 3.1.7 (3).
5. L'état limite ultime se produit lorsque la déformation des armatures atteint la limite εud (Pivot A) et/ou la déformation du béton atteint la limite εcu3 (Pivot B).
Notons le rapport de la profondeur de l'axe neutre/la hauteur effective de la section droite :
| αu = x/d | (b1.1) |
La distribution linéaire des déformations donne :
| αu = εc/(εc + εs) | (b1.2) |
Section frontière AB
On considère une section frontière pour laquelle les pivots A et B sont atteints en même temps : εc = εcu3 et εs = εud.
Dans ce cas, calculons :
| αAB = εcu3/(εcu3 + εud) | (b1.3) |
Si αu > αAB ⇔ le pivot B est atteint en premier. Sinon, le pivot A est atteint en premier.
Section avec armatures tendues élastiques
Au point de départ de la branche supérieure du diagramme contrainte-déformation de calcul pour les aciers de béton armé (voir la Figure 3.8), la déformation vaut εse = fyd/Es.
Calculer :
| αse = εcu3/(εcu3 + εse) | (b1.4) |
Si αu > αse ⇔ l'acier travaille toujours dans la partie élastique. Dans ce cas, le calcul n'est pas économique. Des armatures comprimées sont donc à être ajoutées.
Si αu ≤ αse, aucune armature comprimée n'est nécessaire.
Section avec armatures tendues seules
A l'équilibre, le moment ultime de flexion de calcul doit être équilibré par le moment de résistance de la section :
| MEd = Fc z = b η fcd λ x (d - λ x/2) | (b1.5) |
| MEd = Fs z = As σs (1 - λ αu /2) d ⇔ As = MEd /[(1 - λ αu /2) d σs] | (b1.6) |
Posons :
| μu = MEd /(b d2 η fcd) | (b1.7) |
(b1.5) ⇒ 2 μu = 2 λ (x/d) - λ2 (x/d)2
|
⇔ 2 μu = 2 λ (αu) - λ2 (αu)2 |
(b1.8) |
Si μu ≤ 0,5, cette équation quadratique a une solution :
| αu = [1 - (1 - 2μu)0.5] /λ | (b1.9) |
• αu ≤ αAB ⇒ Pivot A, aucune armature comprimée n'est nécessaire
La déformation dans les armatures tendues εs = εud.
En lisant le diagramme contrainte-déformation pour l'acier de béton armé (voir plus dans 3.2.7 (2))
⇒ la contrainte dans les armatures tendues σs.
(b1.6) ⇒ l'aire de la section d'armatures As.
• αAB < αu ≤ αse ⇒ Pivot B, l'acier travaille dans la partie plastique, aucune armature comprimée n'est nécessaire
La déformation du béton εc = εcu3.
La déformation des armatures tendues :
| εs = εcu3⋅(d - x)/x = εcu3⋅(1 - αu)/αu | (b1.10) |
En lisant le diagramme contrainte-déformation pour l'acier de béton armé
⇒ la contrainte dans les armatures tendues σs.
(b1.6) ⇒ l'aire de la section d'armatures As.
Si μu > 0,5, l'équation quadratique (b1.8) n'a pas de solution.
Dans ce cas, on considère que les armatures tendues seules ne sont pas suffisantes parce que le moment de flexion est trop grand. Il convient de calculer des armatures comprimées.
Section avec deux armatures
• αu > αse ⇒ Pivot B, les armatures tendues ne travaillent pas encore dans la partie plastique, des armatures comprimées sont nécessaires;
• Ou μu > 0,5
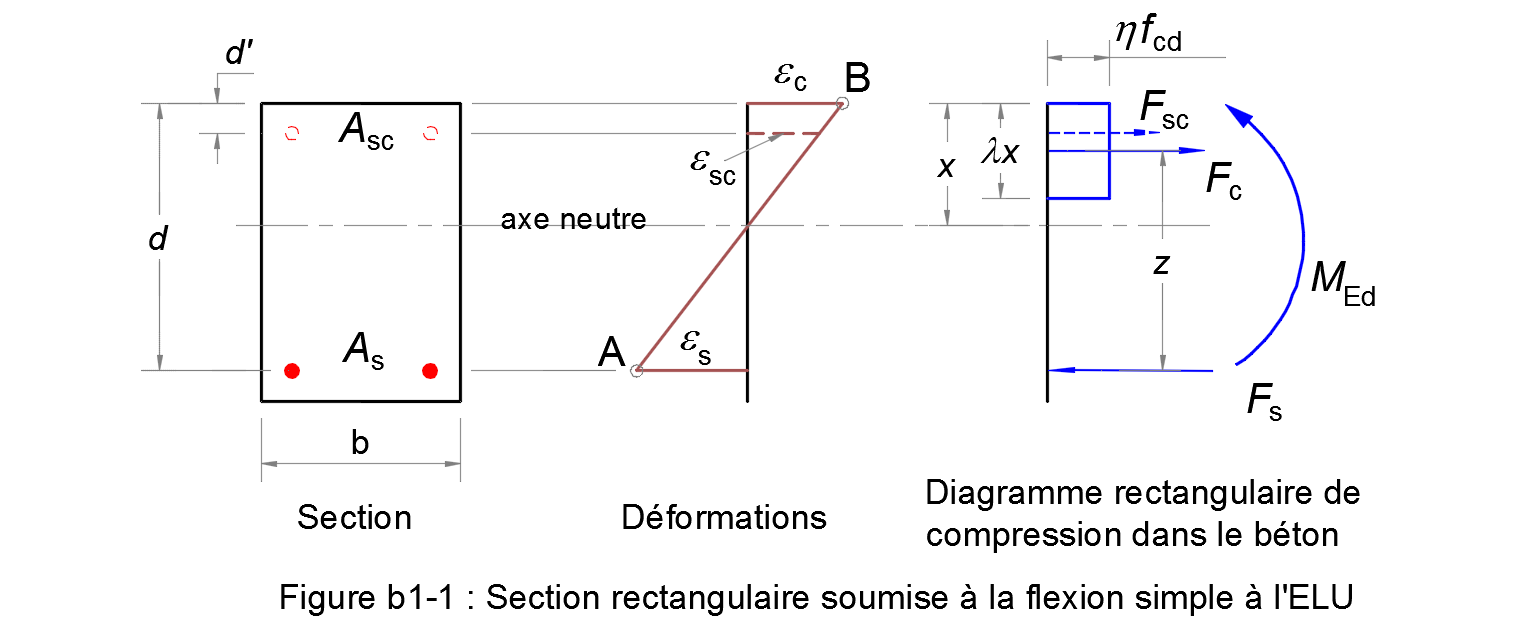
On considère que la section est une superposition de deux sections fictives (voir la Figure b1-2):
- une section de béton avec une partie d'armatures tendues As1 qui a une déformation εs = εse = fyd/Es ;
- une section avec deux armatures seules : As2 et Asc.
Pour la première section:
(b1.4) ⇒ αse; (b1.8) ⇒ μse.
(b1.7) ⇒ le moment de flexion chargé par cette section vaut :
| Mse = μse (b d2 η fcd) | (b1.11) |
(b1.6) ⇒ les armatures tendues As1 = Mse /[(1 - λ αse /2) d fyd].
Pour la deuxième section, à l'équilibre :
| MEd - Mse = Asc (d - d') σsc ⇔ Asc = (MEd - Mse) /[(d - d') σsc] | (b1.12) |
| Fs2 = Fsc ⇔ As2 = Asc σsc /σs2 | (b1.13) |
Le diagramme des déformations de la section ⇒ la déformation des armatures comprimées
εsc = εcu3⋅(αse - d/d')/αse.
En lisant le diagramme contrainte-déforamtion pour les aciers de béton armé
⇒ la contrainte dans les armatures comprimées σsc.
(b1.12) ⇒ l'aire de la section d'armatures comprimées Asc.
σs2 = σs1 = fyd
(b1.13) ⇒ l'aire de la section d'armatures tendues As2.
Finalement, les armatures tendues totales sont égales à :
| As = As1 + As2 | (b1.14) |
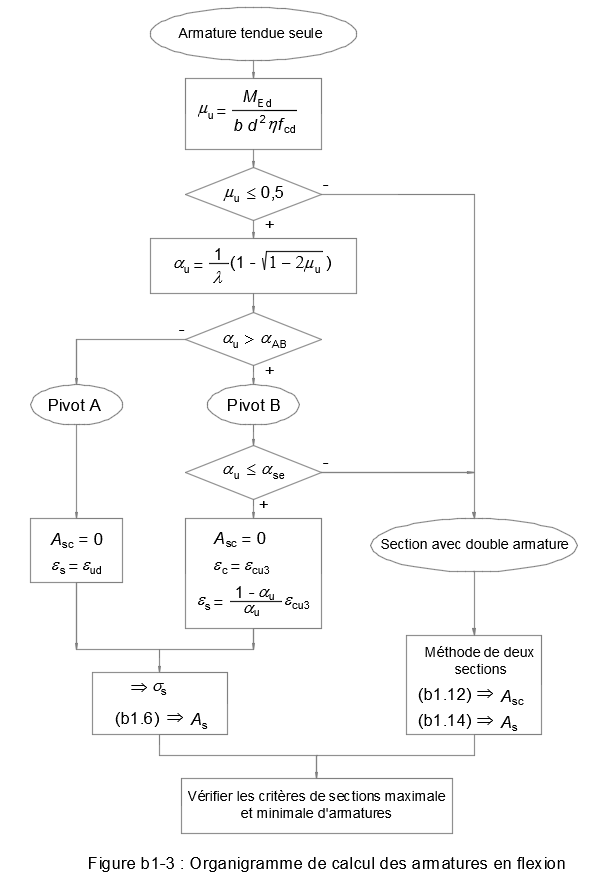
Organigramme
La Figure b1-3 résume cette méthode de calcul des armatures d'une section rectangulaire de béton soumise à la flexion simple :