b3. Méthode de calcul du moment résistant ultime d'une section rectangulaire en flexion simple à l'ELU, MRd
Eurocode 2 - Calcul des sections de béton
Hypothèses
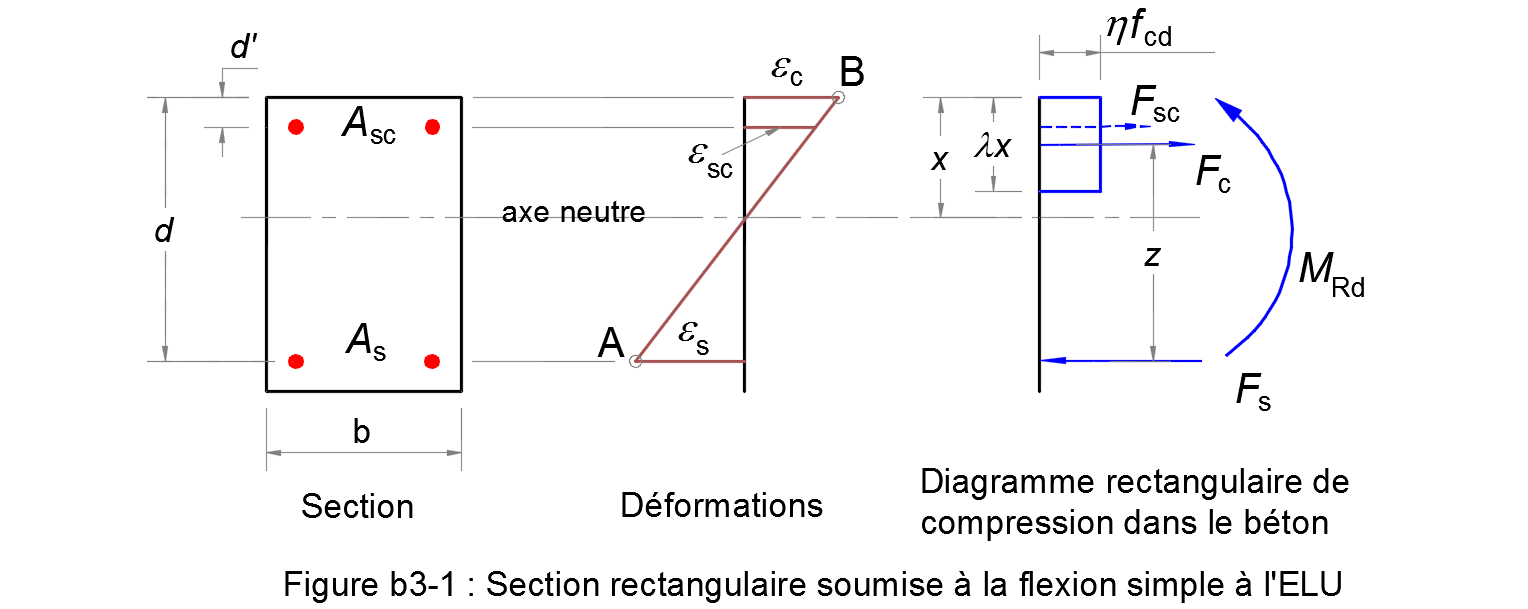
1. La section plane reste plane après déformation. Ainsi, la distribution des déformations est linéaire à travers la section.
2. Les armatures subissent les mêmes déformations que le béton adjacent.
3. La résistance du béton à la traction est négligée.
4. Un diagramme rectangulaire de compression dans le béton est admis, voir 3.1.7 (3).
5. L'état limite ultime se produit lorsque la déformation des armatures atteint la limite εud (Pivot A) et/ou la déformation du béton atteint la limite εcu3 (Pivot B).
Notons le rapport de la profondeur de l'axe neutre/la hauteur effective de la section droite :
| αu = x/d | (b2.1) |
La distribution linéaire des déformations donne :
| αu = εc/(εc + εs) | (b2.2) |
Section frontière AB
On considère une section frontière pour laquelle les pivots A et B sont atteints en même temps : εc = εcu3 et εs = εud.
Dans ce cas, calculons :
| αAB = εcu3/(εcu3 + εud) | (b2.3) |
Si αu > αAB ⇔ le pivot B est atteint en premier. Sinon, le pivot A est atteint en premier.
Calcul itératif du ratio de hauteur comprimée αu
Cette application considère d'/d ≤ αu < 1. Le calcul débute par la valeur minimale αu = d'/d.
• αu ≤ αAB ⇒ Pivot A
La déformation des armatures tendues εs1 = εud.
Le diagramme des déformations ⇒ la déformation des armatures comprimées εsc = εud⋅(αu - d/d')/(1 - αu).
• αu > αAB ⇒ Pivot B
La déformation maximale du béton εc = εcu3.
Le diagramme des déformations ⇒
• La déformation des armatures tendues
εs = εcu3⋅(1 - αu)/αu
• la déformation des armatures comprimées
εsc = εcu3⋅(αu - d/d')/αu.
Le diagramme contrainte-déformation pour l'acier de béton armé
⇒ les contraintes dans les armatures σs, σsc.
A l'équilibre, la somme des forces agissant sur la section donne :
| αu* = (As σs - Asc σsc) / (b λ η fcd d) | (b3.4) |
Il convient de comparer cette valeur calculée de αu* avec la valeur initiale αu. Si la différence est suppérieure à 5 %, on refait le calcul avec une valeur plus importante de αu. Si la différence est inférieure à 5 %, on accepte la valeur initiale αu comme le ratio de hauteur comprimée.
Moment résistant ultime MRd
A l'équilibre, la somme des moments au centre de gravité des armatures tendues donne :
| MRd = Asc σsc (d - d') + b λ x η fcd (d - λ x / 2) | (b3.5) |
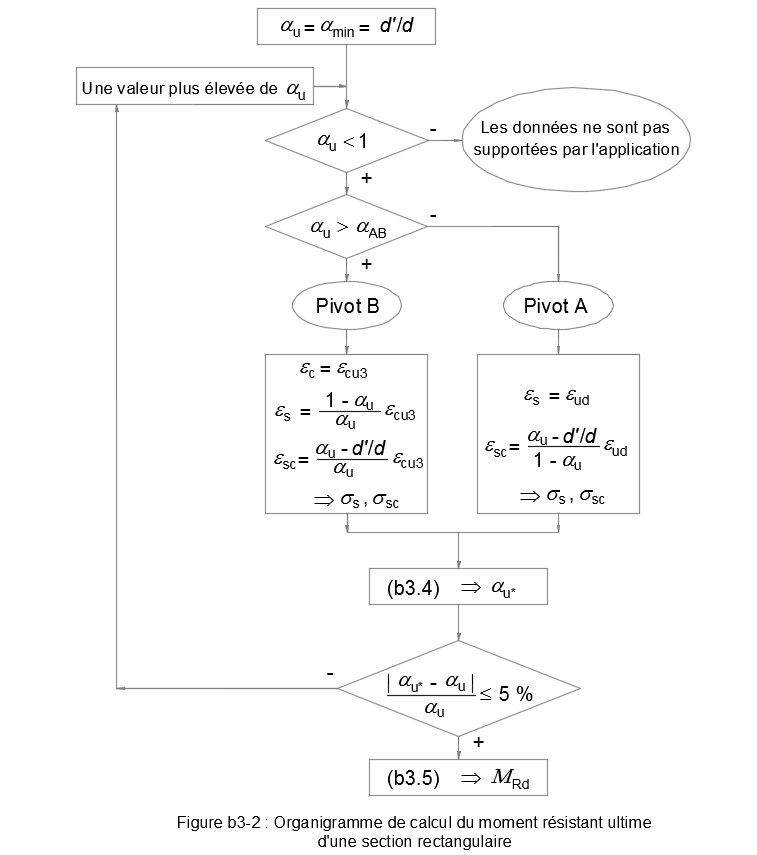
Organigramme
La Figure b3-2 résume cette méthode de calcul du moment résistant ultime d'une section rectangulaire soumise à la flexion simple :