Stress in reinforcing steel depending on its strain, σ_s

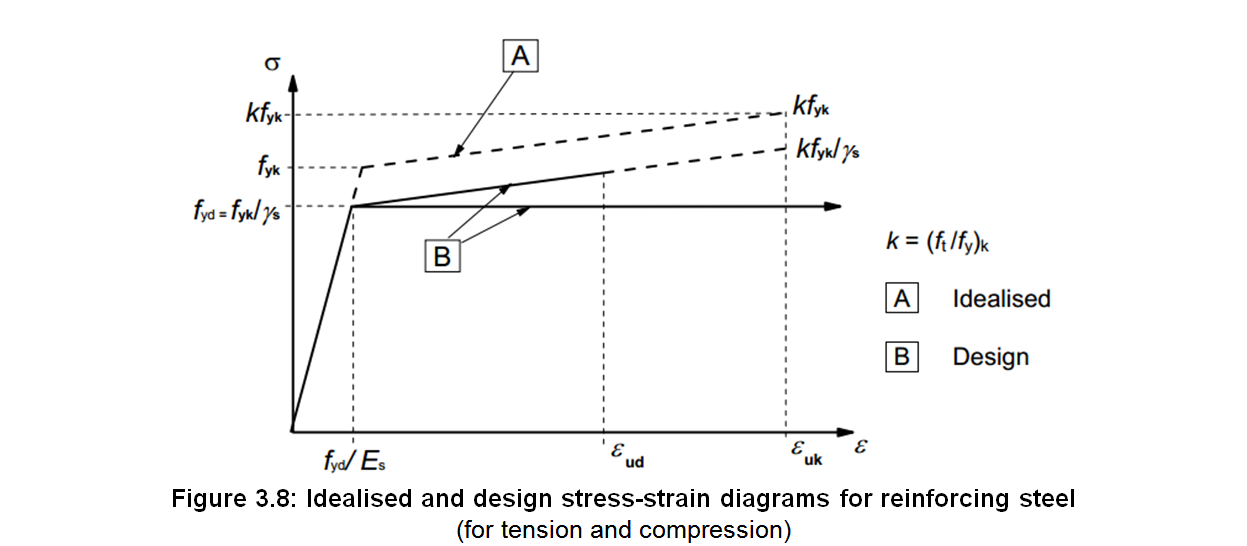
For normal design, either of the following assumptions may be made (see Figure 3.8):

a) an inclined top branch with a strain limit of ε_ud and a maximum stress of kf_yk/γ_S at ε_uk, where k = (f_t/f_y)_k,

b) a horizontal top branch without the need to check the strain limit.

where:

f_yk

is the characteristic yield strength of the reinforcing steel, see § 3.2.2 (3)P.

γ_S

is the partial factor for reinforcing steel, see § 2.4.2.4 (1).

k

is the ductility property, see Table C.1

ε_uk

is the characteristic strain of the reinforcing steel at maximum load, see Table C.1

E_s

is the design value of the modulus of elasticity of the reinforcing steel, see § 3.2.7 (4).

f_yd

is the design yield strength of the reinforcing steel, f_yd = f_yk/γ_S

ε_ud

is the design strain of the reinforcing steel at maximum load, ε_ud  = Coef(ε_ud)⋅ε_uk, see § 3.2.7 (2) for the value of Coef(ε_ud).

If ε_s ≤ ε_se (with ε_se = f_yd/E_s), the stress in reinforcing steel σ_s = E_s⋅ε_s.

If ε_se < ε_s ≤ ε_ud, the stress in reinforcing steel σ_s is equal to:

• f_yd + (ε_s - ε_se)⋅(kf_yk - f_yk)/(ε_uk - f_yk/E_s) for inclined top branch,
• f_yd for horizontal top branch.