Crack control: the minimum reinforcement area A_s,min

If crack control is required, a minimum amount of bonded reinforcement is required to control cracking in areas where tension is expected. The required minimum areas of reinforcement may be calculated as follows:

where:

A_s,min

is the minimum area of the reinforcing steel within the tensile zone

A_ct

is the area of concrete within tensile zone.

σ_s

is the absolute value of the maximum stress permitted in the reinforcement immediately after formation of the crack. This may be taken as the yield strength of the reinforcement, f_yk. A lower value may, however, be needed to satisfy the crack width limits according to the maximum bar size or spacing (cf. 7.3.3 (2))

f_ct,eff

is the mean value of the tensile strength of the concrete effective at the time when the cracks may first be expected to occur:
f_ct,eff = f_ctm or lower, (f_ctm(t)), if cracking is expected earlier than 28 days

k

is the coefficient which allows for the effect of non-uniform self-equilibrating stresses, which lead to a reduction of restraint forces
= 1,0 for webs with h ≤ 300 mm or flanges with widths less than 300 mm,
= 0,65 for webs with h ≥ 800 mm or flanges with widths greater than 800 mm,
intermediate values may be interpolated

k_c

is a coefficient which takes account of the stress distribution within the section immediately prior to cracking and of the change of the lever arm:

* For pure tension k_c = 1,0;
* For bending or bending combined with axial forces:
- For rectangular sections and webs of box sections and T-sections:

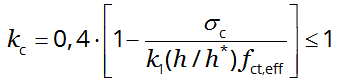
(7.2)

where:

σ_c

is the mean stress of the concrete acting on the part of the section under consideration:

σc = NEd/(b⋅h)

(7.4)

with

N_Ed

the axial force at the serviceability limit state acting on the part of the cross-section under consideration (compressive force positive). N_Ed should be determined considering the characteristic values of prestress and axial forces under the relevant combination of actions

b

the width of the section

h

the height of the section

h^*

h^* = h     for h < 1,0 m
h^* = 1,0 m   for h ≥ 1,0 m

k₁

is a coefficient considering the effects of axial forces on the stress distribution:
k₁ = 1,5     if N_Ed is a compressive force
k₁ = 2h^*/(3h)  if N_Ed is a tensile force

- For flanges of box sections and T-sections:

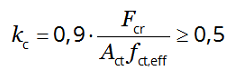
(7.3)

where:

F_cr

is the absolute value of the tensile force within the flange immediately prior to cracking due to the cracking moment calculated with f_ct,eff.