Time dependent losses of prestress due to creep, shrinkage and relaxation, ΔP_c+s+r

A simplified method to evaluate time dependent losses at location x under the permanent loads is given by:

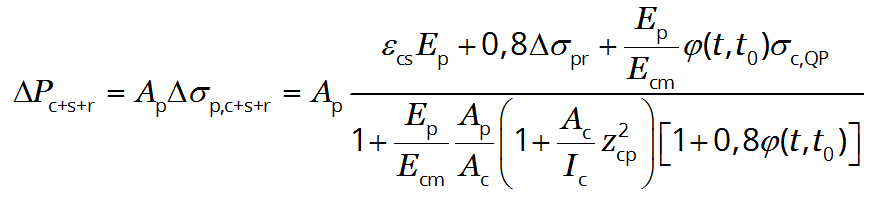(5.46)

where:

Δσ_p,c+s+r

is the absolute value of the variation of stress in the tendons due to creep, shrinkage and relaxation at location x, at time t

ε_cs

is the estimated shrinkage strain, in absolute value

E_p

is the modulus of elasticity for the prestressing steel, see § 3.3.6 (2) and § 3.3.6 (3)

E_cm

is the modulus of elasticity for the concrete

Δσ_pr

is the absolute value of the variation of stress in the tendons at location x, at time t, due to the relaxation of the prestressing steel. It is determined for a stress of σ_p = σ_p(G + P_m0 + ψ₂Q) which is the initial stress in the tendons due to initial prestress and quasi-permanent actions

φ(t,t₀)

is the creep coefficient at a time t and load application at time t₀

σ_c,QP

is the stress in the concrete adjacent to the tendons, due to self-weight and initial prestress and other quasi-permanent actions where relevant

A_p

is the area of all the prestressing tendons at the location x

A_c

is the area of the concrete section

I_c

is the second moment of area of the concrete section

z_cp

is the distance between the centre of gravity of the concrete section and the tendons.

Compressive stresses and the corresponding strains should be used with a positive sign.