Shear between web and flanges: the transverse reinforcement per unit length A_sf/s_f and crushing of the compressive structs in the flanges

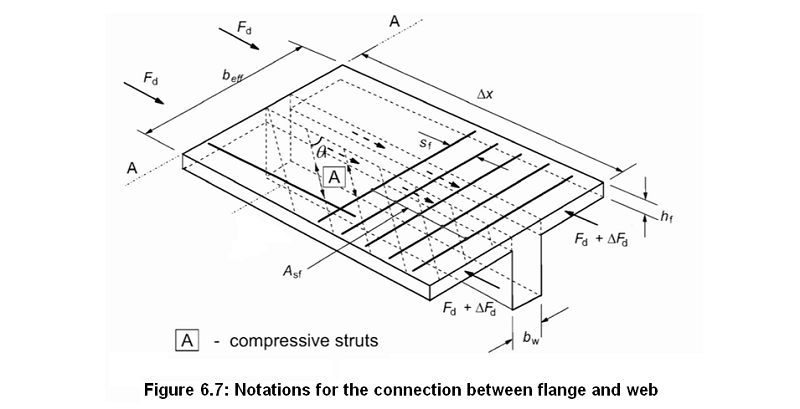
• The transverse reinforcement per unit length, A_sf/s_f, may be determined as follows (see Figure 6.7):

where:

v_Ed

is the longitudinal shear stress at the junction between one side of a flange and the web. It is determined by the change of the normal (longitudial) force in the part of the flange considered:

vEd = ΔFd / (hf⋅Δx)

(6.20)

with

h_f

the thickness of flange at the junctions

Δx

the length under consideration.
The maximum value that may be assumed for Δx is half the distance between the section where the moment is 0 and the section where the moment is maximum. Where point loads are applied the length Δx should not exceed the distance between point loads

ΔF_d

the change of the normal force in the flange over the length Δx.

θ_f

is the angle between the concrete compression strut and the beam axis, see § 6.2.4 (4)

f_yd

is the design yield strength of the reinforcement, f_yd = f_yk/γ_S,
  see § 2.4.2.4 (1), § 2.4.2.4 (2) for the values of γ_S,
  see § 3.2.2 (3)P for the uper limit of f_yk,
  see Figure 3.8 for the design stress-strain diagrams of the reinforcing steel.

• To prevent crushing of the compression struts in the flange, the following condition should be satisfied:

where:

ν

is a strength reduction factor for concrete cracked in shear, the recommended value of ν is ν = 0,6(1 - f_ck/250) (Expression 6.6N in § 6.2.2 (6))

f_cd

is the design compressive strength of concrete, see § 3.1.6 (1)P.