Calculation of crack widths wk
Eurocode 2 part 1-1: Design of concrete structures 7.3 Crack control
The crack width, wk, may be calculated as follows:
| wk = sr,max⋅(εsm - εcm) | (7.8) |
where:
- sr,max
- is the maximum crack spacing
- εsm
- is the mean strain in the reinforcement under the relevant combination of loads, including the effect of imposed deformations and taking into account the effects of tension stiffening
- εcm
- is the mean strain in the concrete between cracks.
The difference of the mean strains εsm - εcm
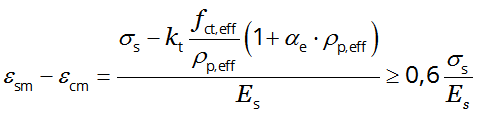 | (7.9) |
where:
- σs
- is the stress in the tension reinforcement assuming a cracked section,
see application for a rectangular section or application for a T-section - Es
- is the design value of the modulus of elasticity of the reinforcing steel, see § 3.2.7 (4)
- αe
- is the ratio Es/Ecm
with
- fct,eff
- is the mean value of the tensile strength of the concrete effective at the time when the cracks may first be expected to occur:
fct,eff = fctm or lower, (fctm(t)), if cracking is expected earlier than 28 days - ρp,eff
-
= (As + ξ1⋅A'p)/Ac,eff (7.10) with
- As
- the cross sectional area of reinforcement
- A'p
- the area of pre or post-tensioned tendons within Ac,eff
- Ac,eff
- the effective area of concrete in tension surrounding the reinforcement or prestressing tendons of depth, hc,ef, where hc,ef is the lesser of 2,5(h - d), (h - x)/3 or h/2 (see Figure 7.1)
- ξ1
- the adjusted ratio of bond strength taking into account the different diameters of prestressing and reinforcing steel:
ξ1 = 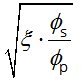
(7.5) with
- ξ
- the ratio of bond strength of prestressing and reinforcing steel, according to Table 6.2
- ΦS
- the largest bar diameter of the reinforcing steel
- ΦP
- the diameter or equivalent diameter of prestressing steel:
Φp = 1,6⋅√AP for bundles, where AP is the area of a prestressing steel,
Φp = 1,75⋅Φwire for single 7 wire strands,
Φp = 1,20⋅Φwire for single 3 wire strands, where Φwire is the wire diameter.
- kt
- is a factor dependent on the duration of the load:
kt = 0,6 for short term loading,
kt = 0,4 for long term loading.
The maximum crack spacing sr,max
• Where the bonded reinforcenlent is fixed at reasonably close centres within the tension zone (spacing ≤ 5(c + Φ/2), cf. Figure 7.2), the maximum crack spacing sr,max may be calculated as follows:
| sr,max = k3c + k1k2k4Φ / ρp,eff | (7.11) |
where:
- Φ
- is the bar diameter. Where a mixture of bar diameters is used in a section, an equivalent diameter, Φeq, should be used.
- c
- is the cover to the longitudinal reinforcement
- ρp,eff
- see the difference of the mean strains above
- k1
- is a coefficient which takes account of the bond properties of the bonded reinforcement:
k1 = 0,8 for high bond bars,
k1 = 1,6 for bars with an effectively plain surface (e.g. prestressing tendons). - k2
- is a coefficient which takes account of the distribution of strain:
k2 = 0,5 for bending,
k2 = 1,0 for pure tension.
Intermediate values of k2 should be used for cases of eccentric tension or for local areas:k2 = (ε1 + ε2)/(2ε1) (7.13) where ε1 is the greater and ε2 is the lesser tensile strain at the boundaries of the section considered, assessed on the basis of a cracked section.
- k3
- is a Nationally Determined Parameter, see § 7.3.4 (3)
- k4
- is a Nationally Determined Parameter, see § 7.3.4 (3).
• Where the spacing of the bonded reinforcement exceeds 5(c + Φ/2) (cf. Figure 7.2), or where there is no bonded reinforcement within the tension zone, the maximum crack spacing sr,max may be calculated as follows:
| sr,max = 1,3(h - x) | (7.14) |
where:
- h
- is the overall depth of the section (see Figure 7.1)
- x
- is the neutral axis depth of the section (see Figure 7.1).
This application calculates the crack width wk from your inputs. Intermediate results will also be given.
First, change the following option if necessary: