Moment of resistance of an uncracked rectangular section in bending at the SLS, M_ct,ser

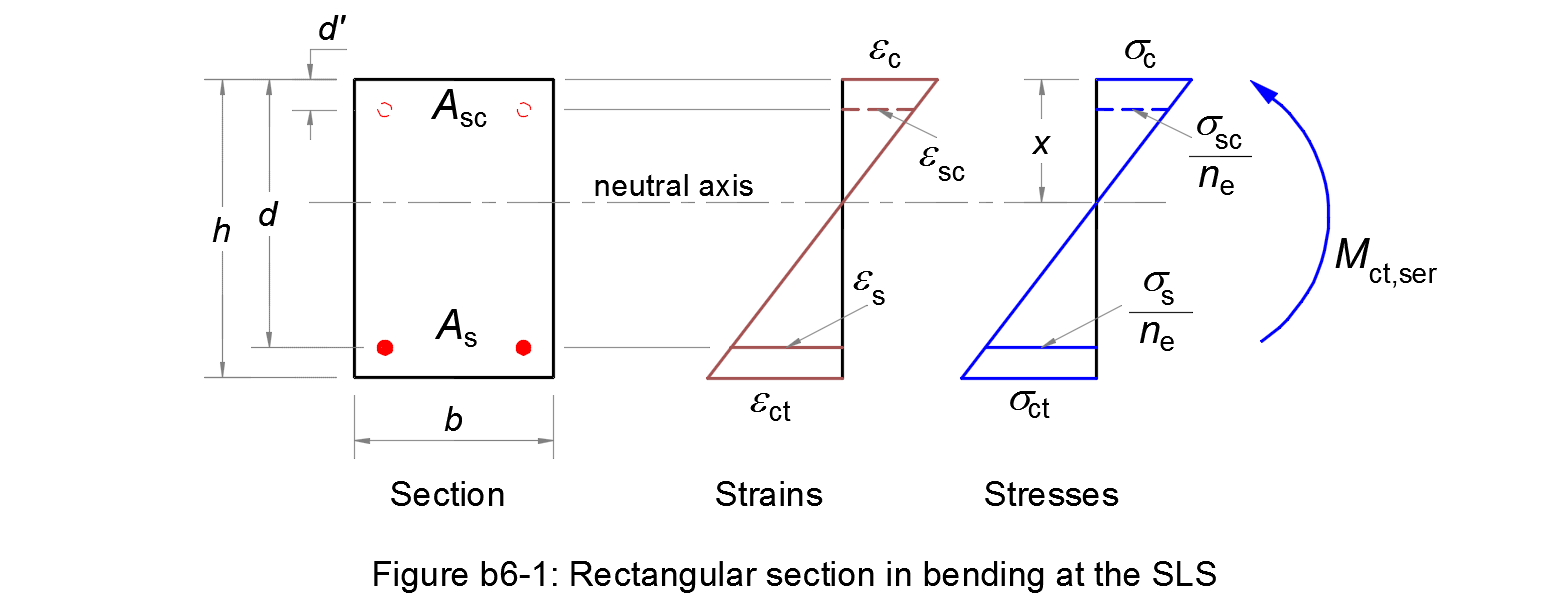
The moment of resistance of an uncracked rectangular section in bending at the SLS is calculated according to method b6.

The parameters needed for the design are the followings:

E_s

is the design value of the modulus of elasticity of the reinforcing steel, see § 3.2.7 (4);

E_c,eff

is the effective modulus of elasticity of concrete;

f_ct,eff

is the mean value of the tensile strength of the concrete effective at the time when the cracks may first be expected to occur:
f_ct,eff = f_ctm or lower, (f_ctm(t)), if cracking is expected earlier than 28 days;

A_sc

is the cross sectional area of the compression reinforcement;

A_s

is the cross sectional area of the tensile reinforcement;

b

is the width of the concrete cross-section;

h

is the height of the concrete cross-section;

d

is the effective depth of the concrete cross-section;

d'

is the distance from the external compressive concrete to the centre of gravity of the compression steel;