Stresses of a rectangular section in bending at the SLS, σ_c and σ_s

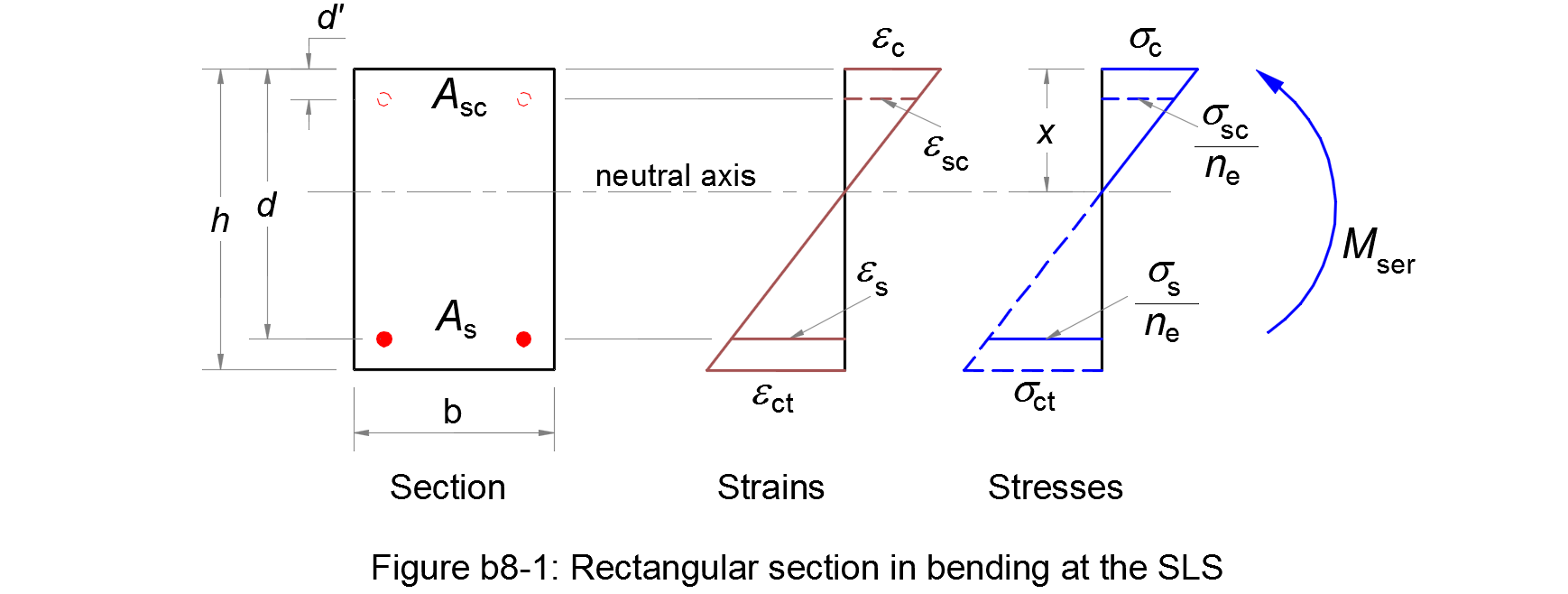
The compressive stress in the concrete σ_c and tensile stress in the reinforcement σ_s of a rectangular section in bending at the SLS are calculated according to method b8.

The parameters needed for the design are the followings:

E_s

is the design value of the modulus of elasticity of the reinforcing steel, see § 3.2.7 (4);

E_c,eff

is the effective modulus of elasticity of concrete;

f_ct,eff

is the mean value of the tensile strength of the concrete effective at the time when the cracks may first be expected to occur:
f_ct,eff = f_ctm or lower, (f_ctm(t)), if cracking is expected earlier than 28 days;

A_sc

is the cross sectional area of the compression reinforcement;

A_s

is the cross sectional area of the tensile reinforcement;

b

is the width of the concrete cross-section;

h

is the height of the concrete cross-section;

d

is the effective depth of the concrete cross-section;

d'

is the distance from the external compressive concrete to the centre of gravity of the compression steel;

M_ser

is the design bending moment at the serviceability limit state.
M_ser is generated by the characteristic combination of loads in case of stress limitation verification (see § 7.2 (2) and § 7.2 (5)).
M_ser is generated by the quasi-permanent combination of loads in case of crack width calculation.