Tensile reinforcement of a rectangular section in bending at the SLS with known compression reinforcement, A_s

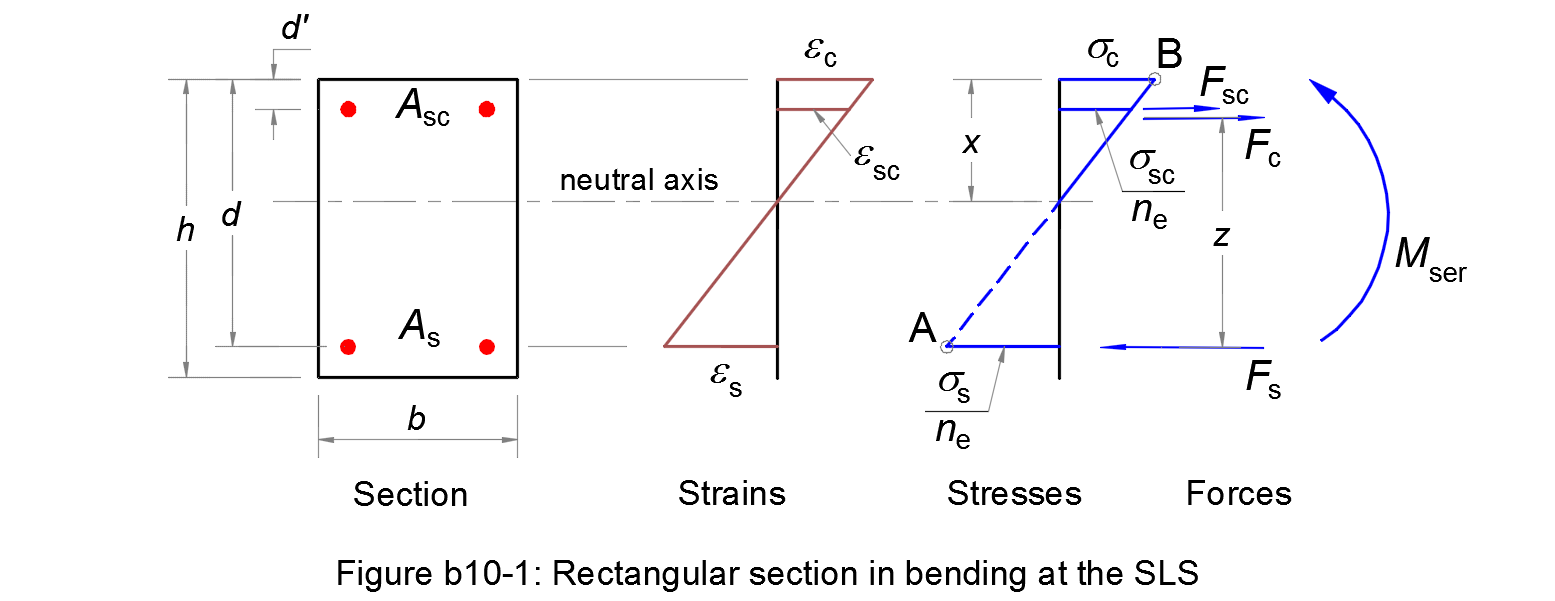
The tensile reinforcement of a rectangular section in bending at the SLS by stress limitation, with known compression reinforcement, are calculated according to method b10.

The parameters needed for the design are the followings:

E_s

is the design value of the modulus of elasticity of the reinforcing steel, see § 3.2.7 (4);

f_yk

is the yield strength of the reinforcing steel, see § 3.2.2 (3)P;

γ_s

is the partial factor for reinforcing steel at the serviceability limit state, see § 2.4.2.4 (2);

k₃

is a Nationally Determined Parameter, see § 7.2 (5);

•

Concrete class: see Table 3.1;

E_c,eff

is the effective modulus of elasticity of concrete;

k₁

is a Nationally Determined Parameter, see § 7.2 (2);

b

is the width of the concrete cross-section;

d

is the effective depth of the concrete cross-section;

d'

is the distance from the external compressive concrete to the centre of gravity of the compression steel;

A_sc

is the cross sectional area of the compression reinforcement;

M_ser

is the design bending moment under the characteristic combination of loads;

The calculated reinforcement should be compared to the minimum and maximum reinforcement requirements for members (slabs, beams, foundations...). Such verification is outside scope of this application.