T-section in bending at the ULS: the longitudinal reinforcements A_sc and A_s

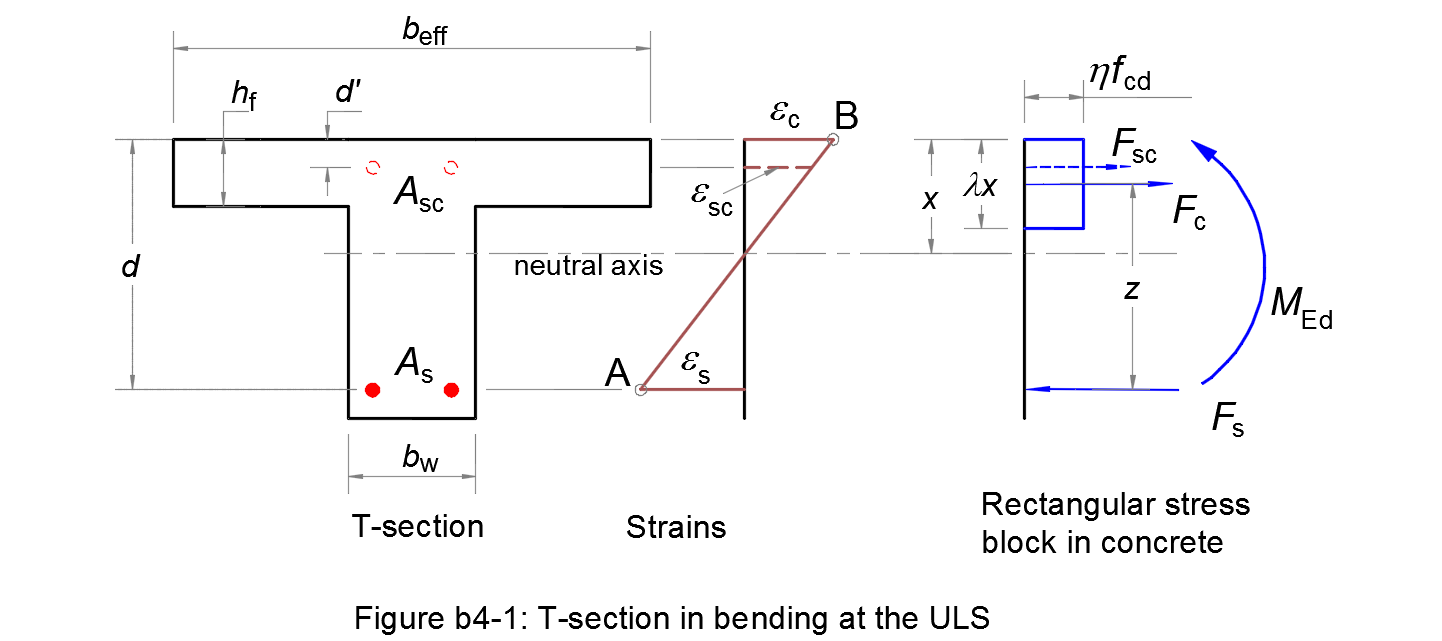
The reinforcements of a T-section in bending at the ultimate limit state are calculated according to method b4.

The parameters needed for the design are the followings:

•

Steel class: see Table C.1. The characteristic strain ε_uk and the ductility property k will be taken equal to their minimum values in the table;

E_s

is the design value of the modulus of elasticity of the reinforcing steel, see § 3.2.7 (4);

f_yk

is the yield strength of the reinforcing steel, see § 3.2.2 (3)P;

γ_s

is the partial factor for reinforcing steel at the ultimate limit state, see § 2.4.2.4 (1);

•

Steel diagram: is the design stress-strain diagram for reinforcing steel, from which the design strain limit ε_ud and the stress in the steel will be defined. See § 3.2.7 (2) and application stress-strain for reinforcing steel;

•

Coef(ε_ud/ε_uk): is chosen by National Annex, see § 3.2.7 (2);

•

Concrete class: see Table 3.1;

f_cd

is the design compressive strength of concrete, see application;

b_w

is the web width of the T-section;

b_eff

is the flange width of the T-section;

h_f

is the flange height of the T-section;

d

is the effective depth of the T-section;

d'

is the distance from the compression fibre to the centre of gravity of the compression steel;

M_Ed

is the design bending moment at the ultimate limit state.

The calculated reinforcements should be compared to the minimum and maximum reinforcement requirements for members (slabs, beams, foundations...). Such verification is outside scope of this application.