Ultimate moment of resistance of a rectangular section in bending, M_Rd

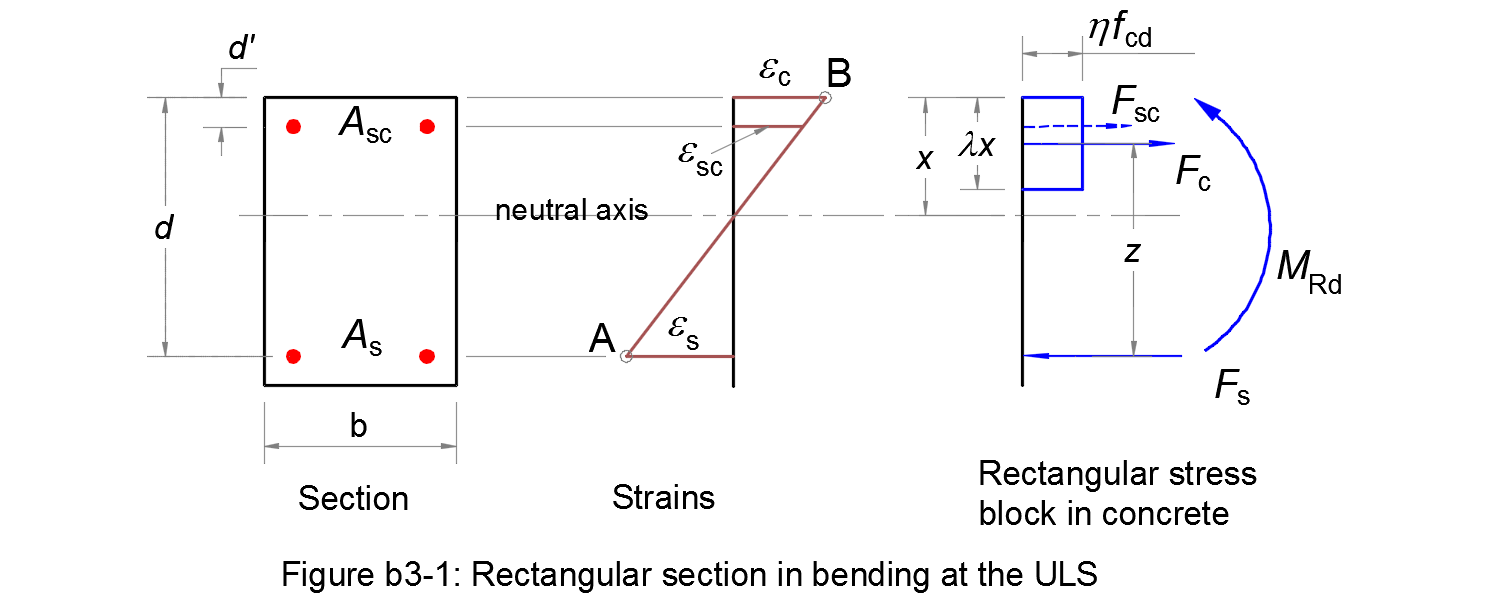
The ultimate moment of resistance of a rectangular section in bending at the ULS are calculated according to method b3.

The parameters needed for the design are the followings:

•

Steel class: see Table C.1. The characteristic strain ε_uk and the ductility property k will be taken equal to their minimum values in the table;

E_s

is the design value of the modulus of elasticity of the reinforcing steel, see § 3.2.7 (4);

f_yk

is the yield strength of the reinforcing steel, see § 3.2.2 (3)P;

γ_s

is the partial factor for reinforcing steel at the ultimate limit state, see § 2.4.2.4 (1);

•

Steel diagram: is the design stress-strain diagram for reinforcing steel, from which the design strain limit ε_ud and the stress in the steel will be defined. See § 3.2.7 (2) and application stress-strain for reinforcing steel;

•

Coef.(ε_ud/ε_uk): is chosen by National Annex, see § 3.2.7 (2);

•

Concrete class: see Table 3.1;

f_cd

is the design compressive strength of concrete, see application;

b

is the width of the concrete cross-section;

d

is the effective depth of the concrete cross-section;

d'

is the distance from the compression fibre to the centre of gravity of the compression steel;

A_s

is the cross sectional area of the tensile reinforcement;

A_sc

is the cross sectional area of the compression reinforcement.