b5. Design method for ultimate moment of resistance of a T-section in bending at the ULS, MRd
Eurocode 2 - Design of concrete sections
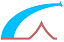
Assumptions
1. Plane sections remain plane after straining, so that there is a linear distribution of strains across the section.
2. Reinforcing steels have the same deformation as the nearby concrete.
3. The tensile strength of concrete is ignored.
4. A rectangular distribution of the compressive stress in the concrete is assumed, see 3.1.7 (3).
5. The ultimate limit state occurs when the strain in the reinforcing steel reaches the limit εud (Pivot A) and/or the strain in the concrete reaches the limit εcu3 (Pivot B).
Considering the depth of the neutral axis/the effective depth of the cross-section:
| αu = x/d | (b5.1) |
The linear distribution of strains gives:
| αu = εc/(εc + εs) | (b5.2) |
Balanced section AB
We consider a balanced section for which the Pivot A and Pivot B are reached at the same time: εc = εcu3 and εs = εud.
For the balanced section, calculating:
| αAB = εcu3/(εcu3 + εud) | (b5.3) |
If αu > αAB ⇔ the Pivot B is reached first. Otherwise, the Pivot A is reached first.
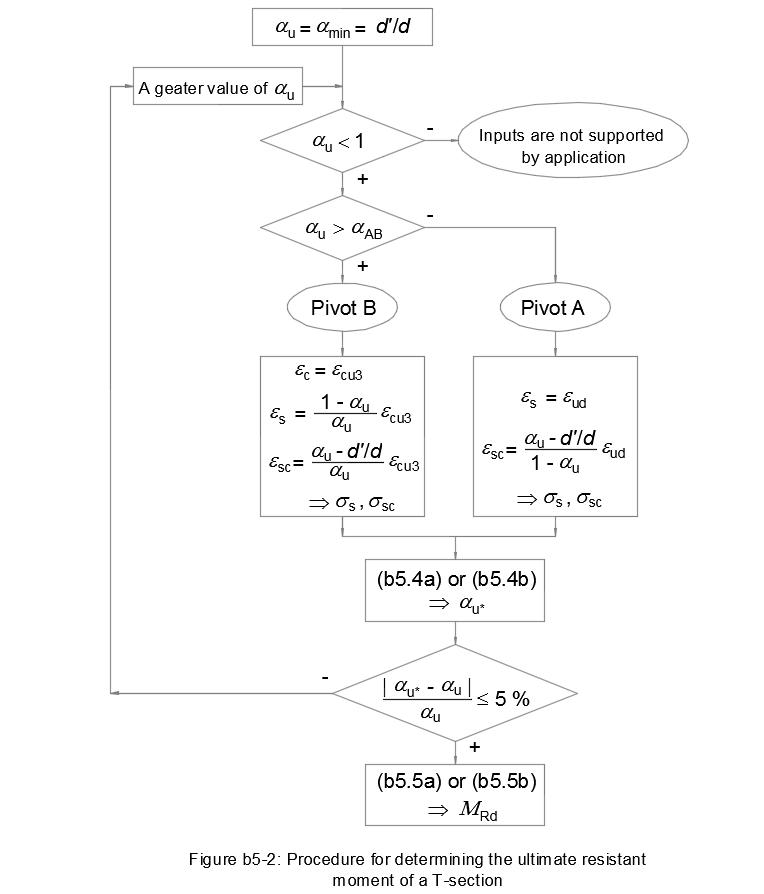
Iterative calculation of the compression depth ratio αu
This application considers d'/d ≤ αu < 1. Beginning by the minimum value αu = d'/d.
• αu ≤ αAB ⇒ Pivot A
The strain in the tensile reinforcement εs1 = εud.
The strain diagram ⇒ the strain in the compression reinforcement εsc = εud⋅(αu - d/d')/(1 - αu).
• αu > αAB ⇒ Pivot B
The strain in the concrete εc = εcu3.
The strain diagram ⇒
• the strain in the tensile reinforcement
εs = εcu3⋅(1 - αu)/αu
• the strain in the compression reinforcement
εsc = εcu3⋅(αu - d/d')/αu.
The design stress-strain diagram for reinforcing steel
⇒ the stresses in the reinforcements σs, σsc.
For equilibrium, the sum of forces acting on the section gives:
| αu* = (As σs - Asc σsc) / (beff d λ η fcd) if αu ≤ hf/d | (b5.4a) |
| αu* = [As σs - Asc σsc - (beff - bw) hf η fcd] / (bw d λ η fcd) if αu > hf/d | (b5.4b) |
This calculated value of αu* must be compared with the initial value αu. If the difference is greater than 5 %, we start over with a greater value of αu. If the difference is lower than or equal to 5 %, we accept the initial value αu as the compression depth ratio.
Ultimate moment of resistance MRd
For equilibrium, the sum of moments to the centre of gravity of the tensile reinforcement gives:
| MRd = Asc σsc (d - d') + beff λ x η fcd (d - λ x / 2) if αu ≤ hf/d | (b5.5a) |
|
MRd =
Asc σsc (d - d') +
bw λ x η fcd (d - λ x / 2) + (beff - bw) hf η fcd (d - hf/2) if αu > hf/d |
(b5.5b) |
Flowchart
Figure b5-2 resumes this design method for a reinforced concrete T-section in bending at the ULS: