b9. Design method for longitudinal reinforcements of a rectangular section in bending at the SLS, `A_sc` and `A_s`

Eurocode 2 - Design of concrete sections

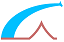
Figure b9-1 introduces a reinforced concrete section with notations. The reinforcements A_sc and A_s are unknown.

Assumptions

1. Plane sections remain plane after straining, so that there is a linear distribution of strains across the section.

2. Reinforcing steels have the same deformation as the nearby concrete.

3. The tensile strength of concrete is ignored.

4. A triangular distribution of the compressive stress in the concrete is assumed.

5. The serviceability limit state occurs when the tensile stress in the reinforcement reaches the limit σ_s,ser = k₃ f_yk (Pivot A) and/or the compressive stress in the concrete reaches the limit σ_c,ser = k₁ f_ck (Pivot B). The parameters k₁ and k₃ are chosen by National Annex, see § 7.2 (2) and § 7.2 (5) respectively.

Considering the depth of the neutral axis/the effective depth of the cross-section:

α_ser = x/d

(b9.1)

The linear distribution of strains and the stress diagram gives:

α_ser = ε_c/(ε_c + ε_s) = n_e σ_c/(n_e σ_c + σ_s)

(b9.2)

where:

n_e

is the effective modular ratio
n_e = E_s / E_c,eff

with:

E_s: the design value of the modulus of elasticity of the reinforcing steel, see § 3.2.7 (4)
E_c,eff: the effective modulus of elasticity for concrete.

Balanced section AB

We consider a balanced section for which the Pivot A and Pivot B are reached at the same time: σ_s = σ_s,ser and σ_c = σ_c,ser.

For the balanced section, calculating:

α_AB = n_e σ_c,ser/(n_e σ_c,ser + σ_s,ser)

(b9.3)

If α_ser > α_AB ⇔ the Pivot B is reached first. Otherwise, the Pivot A is reached first.

Serviceability limit state at Pivot B

For equilibrium, the ultimate design moment must be balanced by the moment of resistance of the section:

M_ser = F_c z = 0,5 b σ_c,ser x (d - x/3) = 0,5 b d² σ_c,ser α_c,ser (1 - α_c,ser/3)

(b9.4)

Substituting the following in (b9.4):

μ_c,ser = M_ser /(b d² σ_c,ser)

(b9.5)

(b9.4) ⇒ μ_c,ser = 0,5 α_c,ser ( 1 - α_c,ser/3)

⇔ α_c,ser² - 3 α_c,ser + 6 μ_c,ser = 0

(b9.6)

If μ_c,ser ≤ 0,375, this quadratic equation has a solution:

α_c,ser = 1,5 [1 - (1 - 8 μ_c,ser/3)^0.5]

(b9.7)

Serviceability limit state at Pivot A

For equilibrium, the ultimate design moment must be balanced by the moment of resistance of the section:

M_ser = F_c z = 0,5 b σ_c x (d - x/3) = 0,5 b d² σ_c α_s,ser (1 - α_s,ser/3)

(b9.8)

The stress σ_c is deducted from the stress diagram:

σ_c = σ_s,ser α_s,ser /[n_e (1 - α_s,ser)]

(b9.9)

Calculating:

μ_s,ser = M_ser /(b d² σ_s,ser)

(b9.10)

Substituting (b9.9) and (b9.10) in (b9.8),
(b9.8) ⇒ μ_s,ser = 0,5 n_e α_s,ser² ( 1 - α_s,ser/3)

⇔ α_s,ser³ - 3 α_s,ser² - 6 n_e μ_s,ser α_s,ser + 6 n_e μ_s,ser = 0

(b9.11)

By solving this cubic equation, we get a root α_s,ser ∈ (0,1).

• α_c,ser > α_AB ⇒ Pivot B

The tensile reinforcement A_s may be determined in two ways:

Based solely on the Pivot B and no compressive reinforcement will be provided;
Based on the balanced section AB. Thus, the tensile reinforcement A_s is optimized because its stress σ_s is taken equal to the limit σ_s,ser. This optimization requires a calculation of the compressive reinforcement A_sc.

In the first case, the tensile stress in the reinforcement is deducted from the stress diagram:

σ_s = n_e σ_c,ser (1 - α_c,ser) /α_c,ser

(b9.12)

The equilibrium of the section allows the calculation of the tensile reinforcement:

A_s = M_ser / [σ_s d (1 - α_c,ser/3)]

(b9.13)

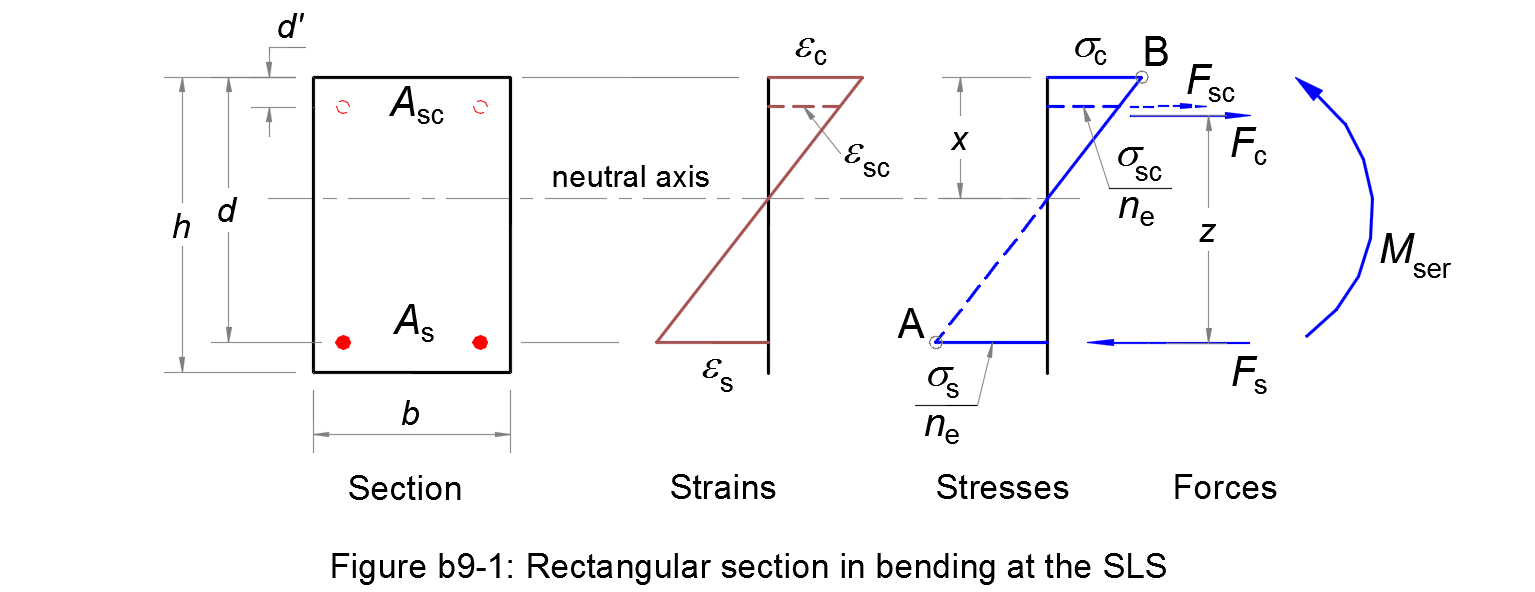
In the second case, we consider that the section is an overlap of two fictive sections (see Figure b9-2):

One concrete section with only a tensile reinforcement A_s1 This section reaches the Pivot A and Pivot B at the same time (balanced section).
One section with only two reinforcements A_s2 and A_sc.

Doubly-reinforced-rectangular-concrete-section-bending-serviceability-limit-state

The bending moment supported by the first section is equal to:

M_AB = 0,5 b d² α_AB σ_c,ser (1 - α_AB/3)

(b9.14)

The tensile reinforcement A_s1 of the first section:

A_s1 = M_AB /[σ_s,ser d (1 - α_AB/3)]

(b9.15)

The tensile reinforcement A_s2 of the second section:

A_s2 = (M_ser - M_AB) /[σ_s,ser (d - d')]

(b9.16)

The compressive stress in the reinforcement:

σ_sc = σ_s,ser [α_AB - d'/d) /(1 - α_AB)]

(b9.17)

The compressive reinforcement A_s2:

A_sc = A_s2 σ_s,ser /σ_sc

(b9.18)

Finally, the total tensile reinforcement is equal to:

A_s = A_s1 + A_s2

(b9.19)

• α_c,ser ≤ α_AB ⇒ Pivot A

No compressive reinforcement is needed.

The tensile reinforcement is calculated using α_s,ser from (b9.11):

A_s = M_ser /[σ_s,ser d (1 - α_s,ser/3)]

(b9.20)

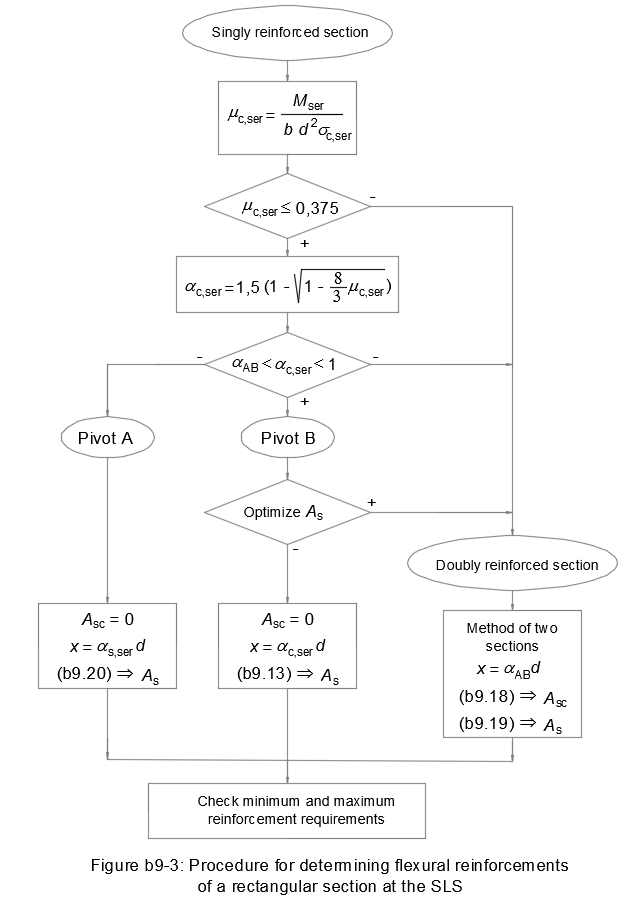
Flowchart

Figure b9-3 resumes this design method for a rectangular reinforced concrete section in bending at the serviceability limit state:

Procedure-reinforcements-rectangular-concrete-section-bending-serviceability-limit-state